Astronomie - Zeitgleichung

Die Zeitgleichung

Zeitgleichung = Mittlere Ortszeit - Wahre Sonnenzeit

Die Messung der Zeit ist für den Menschen schon seit jeher von großer Bedeutung. Sie strukturiert seinen Tagesablauf und gestattet ihm, Tätigkeiten gezielt durchzuführen. Zeit und Termin sind ein gemeinsamer Nenner, unter dem sich die Gesellschaft organisiert.

Bereits in der Antike wußten die Gelehrten, daß die Sonne in ihrem Tageslauf, über das ganze Jahr betrachtet, Abweichungen zeigt. Wir haben gelernt, daß die Sonne morgens im Osten aufgeht, mittags im Süden ihren Höchststand hat und abends im Westen untergeht. Und so erwarten wir, daß die Sonne, wenn es auf unseren Uhren zwölf Uhr ist, die Sonne genau im Meridian (im Süden) steht.

Wir machen die Probe aufs Exempel, setzen eine Kamera mit kurzer Brennweite auf ein Stativ, richten sie nach Süden aus und schießen pro Monat ein Foto, wobei wor extrem unterbelichten (Vorsicht vor erhöhter Sonneneinstrahlung!) oder, das wäre der Idealfall, eine Sonnenschutzfolie vors Objektiv setzen. Die Sonne sollte als Objekt deutlich erkennbar sein. Günstig, aber nicht erforderlich ist es, wenn die erste Aufnahme am Winteranfang oder am Sommeranfang entsteht. Es macht auch nichts, wenn die Abstände zwischen den Aufnahmen ungleich groß sind; wichtig ist nur, daß jedes Foto zur gleichen Tageszeit, am besten, wenn die Turmuhr zwölf schlägt.

Nach Ablauf eines Jahres legen wir alle Aufnahmen mit Hilfe eines geeigneten Bildverarbeitungsprogramms übereinander; als Paßmarken dienen uns dabei etwa Bäume oder Gebäude.

Das Ergebnis überrascht uns dann doch etwas, denn das Gebilde, das die einzelnen Sonnenpunkte zeichnen, erinnert stark an eine schiefstehende Acht (Mauszeiger über das Bild legen!). Wir stellen fest, daß sich die Sonne um 12:00 nie an der gleichen Stelle aufhält. (Weshalb sie nie genau im Süden steht, erkläre ich weiter unten.) Daß sie mal höher, mal niedriger im Zenit steht, können wir uns erklären; das hängt mit den Jahreszeiten zusammen. Aber weshalb bummelt sie mal, und mal hat sie es eilig?

Die Ursache, wir ahnen es, ist nicht die Sonne, denn nicht sie zieht ihre Bahn um die Erde, sondern die Erde um die Sonne. Wir erinnern uns, was Kepler vor langer Zeit bereits herausgefunden hat: Die Erdbahn ist kein Kreis, sondern beschreibt eine Ellipse, in deren einem Brennpunkt sich die Sonne befindet. Außerdem, so Kepler, überstreicht die Erde in ihrem Umlauf in gleichen Zeitabschnitten gleiche Flächen.

Was bedeutet das, und wie bringen wir Keplers Gesetze und unser Analemma - so heißt diese »Acht« - in Zusammenhang?

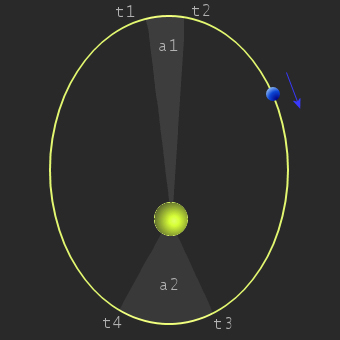
Wir machen eine Reise, so daß wir von oben auf Sonne und Erde herabsehen können. Ist die Erde weit von der Sonne entfernt (wir erinnern uns: Die Erdbahn ist eine Ellipse), lassen wir die Stoppuhr laufen, und nach einer frei wählbaren Zeit (etwa ein Monat) halten wir sie an. Dann hat die Erde den Weg von P1 nach P2 zurückgelegt. Jetzt haben wir Freizeit, bis die Erde in Sonnennähe gelangt ist. Wieder lassen wir die Stoppuhr die gleiche Zeit wie zuvor laufen. In dieser Zeit hat sich die Erde von P3 nach P4 bewegt.

Könnten wir die Flächen A1 und A2 messen, würden wir feststellen, daß sie tatsächlich gleich groß sind. Aber noch etwas Wesentliches sehen wir: Im Vergleich zur Sonnenferne legt die Erde einen längeren Weg zurück, wenn sie sich in Sonnennähe befindet.

Und so wissen wir, mittlerweile auf die Erde zurückgekehrt, weshalb die Sonne auf ihrer scheinbaren Bahn längst den Meridian überquert hat, wenn die Turmuhr schlägt. Ist die Erde dagegen in Sonnenferne, überquert die Sonne den Meridian erst, wenn die Turmuhr längst zwölf geschlagen hat. Wir sollten uns aber nicht zu früh freuen; das ist noch nicht alles.

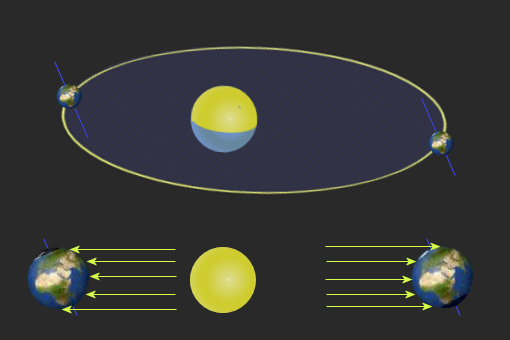
Noch etwas hat Einfluß auf den ungleichmäßigen »Lauf« der Sonne, und wieder hat es mit der Erde zu tun: Die (gedachte) Achse, um die sich die Erde dreht, und die durch Nord- und Südpol verläuft, steht schief auf der Umlaufbahn der Erde. Genauer gesagt: um etwa 23° geneigt.

Diesem Effekt haben wir die Jahreszeiten zu verdanken, denn die Sonne scheint vorrangig auf die Nordhälfte der Erde und steht dort höher am Horizont, wenn sich die Erde in Sonnenferne aufhält, denn dann ist der Nordpol zur Sonne hin geneigt - es ist Sommer auf der Nordhalbkugel und Winter "down under".

Diese beiden Effekte sind also die Ursache des Phänomens: Die nicht konstante Umlaufgeschwindigkeit der Erde verursacht zeitliche Abweichungen von maximal +/- 8 min, während die zur Bahnebene schräg stehende Rotationsachse der Erde für Differenzen von bis zu +/- 10 min verantwortlich ist.

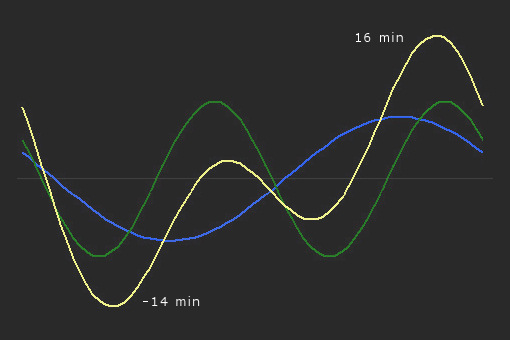
Betrachtet man beide Effekte getrennt voneinander und stellt sie grafisch dar, erhält man jeweils eine Sinuskurve, die grüne für die Abweichungen infolge der schiefen Erdachse, die blaue für die ungleiche Bahngeschwindigkeit.

Beide Effekte überlagern einander; die daraus resultierende gelbe Linie stellt die Zeitgleichung im Verlauf eines Jahres dar.

An vier Tagen des Jahres, am 15. April, 13. Juni, 1. September und 25. Dezember, stimmt also die mittlere Ortszeit mit der wahren Sonnenzeit überein. Die maximale Abweichung nach unten wird mit -14 min am 11. Februar erreicht. Um fast eine Viertelstunde hinkt die Sonne den Uhren hinterher, während sie am 3. November über 16 min vorausläuft.

Eines müssen wir noch klären; weshalb das Analemma (die »Acht«) auf unserem Bild oben immer östlich des Meridians steht: Die Erde ist in verschiedene Zeitzonen unterteilt, und in jeder Zeitzone gilt eine einheitliche Zeit. Bezugspunkt unserer Mitteleuropäischen Zeit (MEZ) ist der 15. Grad östlicher Länge, der mitten durch Görlitz führt.

Zwischen Görlitz und Aachen liegen neun Breitengrade. Nun dreht sich ja die Erde, und wir rechnen schnell aus, daß die Erde für diese 9° etwa 36 min benötigt. Und da die Sonne bekanntlich im Osten aufgeht, geschieht das in Görlitz rund eine halbe Stunde früher als in Aachen, und wenn sie dort im Zenit steht, befindet sie sich in Aachen zur gleichen Zeit noch neun Grad östlich des Zenits.

Um also die mittlere Ortszeit unseres Standorts zu ermitteln, müssen wir von unserer Uhrzeit noch einmal einige Mnuten abziehen, wenn wir uns westlich von Görlitz befinden (in Aachen 36 min), und addieren, sind wir westlich von Görlitz.